Compressor mass flow: Unterschied zwischen den Versionen
| Zeile 69: | Zeile 69: | ||
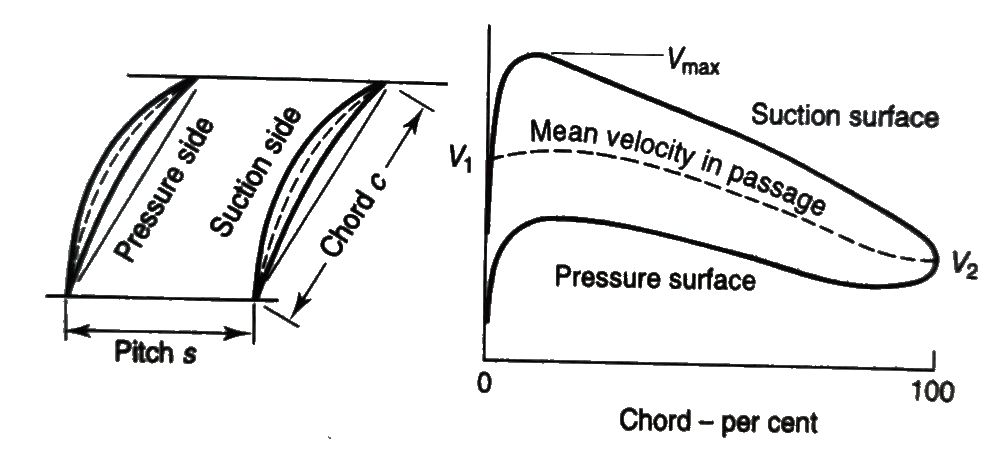
| − | [[File:velocity profile2.jpg|center|200px|frame| | + | [[File:velocity profile2.jpg|center|200px|frame|Typical variation of the velocity profile along the chord. Note that a velocity gradient exists also along the pitch]] |
Version vom 25. Februar 2021, 20:57 Uhr
Inhaltsverzeichnis
1. Introduction
Gas turbine engine certification requires good knowledge of the compressor surge margin. While the working and surge line are easily measurable on a test rig, mass flow measurement is not usually possible in the installed condition. This gives rise to uncertainty on the actual surge margin available for operability manoeuvres. A method to derive the mass flow parameter during transient operation is being proposed. Validation and standardisation of this method would provide a complementary tool for compressor specification. Feedback is requested so as to better evaluate the usefulness of such a standard within the gas turbine community.
2. Background
Gas turbine engine certification requirements stipulate that the compressor should have sufficient margin to avoid surge during operation. Hence proper characterisation of a compressor's surge line in its installed condition is inherent to the certification process.
Compressor mapping on a dedicated test rig is a common practice. This type of test is the basis for verification that the physical unit corresponds to the engineering design and compliant with the specifications. The test rig is sufficiently equipped such that accurate measurements can be made at any working point on the corresponding compressor map. This makes it practical to verify the compressor characteristics namely: reduced mass flow vs pressure ratio, reduced mass flow vs speed, pressure ratio vs speed.
Installation of the compressor into its working environment (a gas turbine for example) may modify its characteristics in unexpected ways due to interactions with the engine architecture features such as a swan-neck duct, bleed holes, back pressure from the internal air circuit, variation in clearances etc. Operating at different altitudes and ambient conditions may also give rise to Reynolds number effects, adversely influencing the compressor surge margin. This rig to engine variation is often difficult to quantify during operability testing, principally because an independent measurement of the mass flow is not possible in the installed condition.
A method for calculating mass flow on an installed compressor is being proposed. The technique relies on measuring the local Mach number at a given segment (between two stator blades) of know area to compute flow. This derived parameter, together with pressure, temperature and shaft speed measurements enable the positioning of the dynamic compressor running line during transient manoeuvres. Thus the compressor's surge-free zone can mapped.
Laying out a validated guideline for this method could be a way to complement existing industry standards. This would delineate a recommanded practice guide for (1) the design and calibration of instrumentation, as well as (2) the implementation of a dedicated calculation routine. Substantiation would be achieved by running a series of back to back compressor tests permitting the comparison between test rig and test bed results.
3. Aerodynamic Theory
In this section, the principles for deriving the compressor map characteristics using common aerodynamic equations is set out.
The derivation is based on the knowledge of the below parameters:
| Parameter | Symbol | Units | Measuring device |
|---|---|---|---|
| Total Pressure | Pt | bar | Total Pressure Probe |
| Static Pressure | ps | bar | StaticPressure Probe |
| Total Temperature | Tt | K | Thermocouple |
| Shaft speed | n | rpm | Rotating speed sensor |
| Specific Heats | Cp, Cv, γ, R | - | Thermodynamic Tables |
| Section Area | A | m2 | Physical geometrical measurement |
The following nomenclature is used in the subsequent equations:
M = mach number c = speed of sound (m/s) ts = static temperature (K) v = local velocity (m/s) ṁ = mass flow (kg/s) ρ = density (kg/m3)
Hence using the principles of one dimensional aerodynamic flow the local velocity and mass flow may be derived as follows
M = fn(Pt, ps)
c = fn(T)
ts = fn(Tt,M) ρ = fn(ps,ts) ṁ = ρAv
Compressor maps are normally presented using reduced parameters, thus:
Reduced Mass Flow = fn(ṁ,Tt,ts,Pt,ps) Pressure Ratio = Pt/Ps Shaft speed = fn(n,Tt)
4. Practical considerations
The simple derivation discussed above does not take into account the three dimensional nature of the flow through the compressor. Pressure and temperature profiles will exist along
• the blade height • in span-wise (pitch-wise) direction between two stators • along the chord length